Math'φsics

Menu
  • Acceuil
  • Maths
  • Physique
    • Maths
    • Physique
  • Information mutuelle conditionnelle

    Formulaire de report


    Information mutuelle entre \(X\) et \(Y\) sachant \(Z\) Quantité définie par : $$I(X;Y|Z)=\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}\sum_{z\in\mathcal Z}p_{XYZ}(x,y,z)\log_2\left(\frac{p_{XY|Z}(x,y|z) }{p_{X|Z}(x|z)p_{Y|Z}(y|z)}\right)$$
    • correspond à l'information commune à \(X\) et \(Y\) lorsque \(Z\) est connu
    • \(I(X;Y|Z)\geqslant\) \(0\), avec égalité si et seulement si \(X\to Z\to Y\) est une Chaîne de Markov
    • on a les formules :
            
      1. \(I(X;Y|Z)=\) \(H(X|Z)+H(Y|Z)-H(X,Y|Z)\)

        
  • \(I(X;Y|Z)=\) \(H(X|Z)-H(X|Y,Z)=H(Y|Z)-H(Y|X,Z)\)


    • Questions de cours

    Montrer que \(I(X;Y|Z)\geqslant\) \(0\), avec égalité si et seulement si \(X\to Z\to Y\) est une Chaîne de Markov.

    On remarque qu'il s'agit d'une Divergence de Kullback-Leibler, et on applique l'Inégalité de Gibbs.

    La nullité a lieu si \(X\) et \(Y\) sont indépendantes conditionnellement à \(Z\) \(\to\) chaîne de Markov.


    START
    Ω Basique (+inversé optionnel)
    Recto: Comment représenter l'information mutuelle conditionnelle dans un diagramme de Venn ?

    Verso:

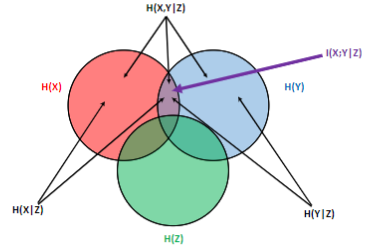
    Bonus:
    Carte inversée ?:
    END
    START
    Ω Basique (+inversé optionnel)
    Recto: Explique pourquoi on ne peut pas toujours utiliser un diagramme de Venn pour justifier une majoration.

    Verso: Le diagramme de Venn est trompeur, car il laisse penser que toutes les parties sont positives.
    Or, rien ne justifie que le coeur du diagramme est positif (il ne correspond à aucune vraie valeur, donc pas d'Inégalité de Gibbs ou quoi).
    Bonus:
    Carte inversée ?:
    END
    START
    Ω Basique (+inversé optionnel)
    Recto: Donner une caractérisation d'une chaîne de Markov \(X\to Y\to Z\).
    Verso: $$I(X;Z|Y)=0$$
    Bonus:
    Carte inversée ?:
    END

    Exercices

    On considère une chaîne de Markov \(X\to Y\to Z\).
    Montrer que \(Z\to Y\to X\) forment également une chaîne de Markov.

    Utiliser la caractérisation via l'information mutuelle conditionnelle.


    Trouver des v.a. Binaires \(X,Y,Z\) tq $$I(X;Y|Z)\lt I(X;Y)$$

    Trois v.a. Égales suffisent.


    Trouver des v.a. Binaires \(X,Y,Z\) tq $$I(X;Y|Z)\gt I(X;Y).$$

    On prend \(X,Y\) indépendantes, et \(Z\) qui permet toujours de déduire l'une en connaissant l'autre.


    START
    Ω Basique (+inversé optionnel)
    Recto: Que peut-on déduire des inégalités suivantes ? $$I(X;Y|Z)\lt I(X;Y)\quad\text{ et }\quad I(X;Y|Z)\gt I(X;Y).$$
    Verso: Conditionner réduit l'entropie, mais a une action inconnue sur l'information mutuelle.
    Bonus:
    Carte inversée ?:
    END
    'information